D-Waveのサンプリング機能を使って最適解群を求める（Max Cut）

D-Waveシステムは量子アニーリングを使用して、エネルギー関数の最小値を求めることで問題を解きます。複数の量子アニーリングが異なる解を返す可能性があるため、問題を「サンプリング」し、返された結果の最低エネルギーの解を調べることができます。

ここでは、最大カット(Max Cut)問題を例にとって、D-Waveシステムのサンプリング機能のご紹介をいたします。1つのグラフ内にある頂点を2つのグループに分割し、グループ間の接続数を最大にする頂点の組み合わせ（言い換えれば、頂点と頂点を接続する辺をカットして、頂点を2つのグループに分割する際に「カットされる辺の本数を最大にする」頂点の組み合わせ）をD-Waveシステムを使って求めます。

D-WaveのOcean SDKを使用して、この問題例を解くプログラムを作成し、D-Waveシステムでアニーリングします。 Ocean SDKは、D-Wave量子コンピューターをプログラミングするためのオープンソースのPythonツールのセットです。

Ocean SDKについては、以下のリンクをご参照ください。

• GitHub上のOcean SDK：https://github.com/dwavesystems/dwave-ocean-sdk
• ドキュメント：https://docs.ocean.dwavesys.com/en/latest/

以下に示されている結果では、その一部に最適には及ばないものがあることがわかります。 D-Waveシステムは確率的であるため、通常、返された結果の間で回答の分布が見られ、その一部は最適ではない場合があります。このため、ほとんどの場合、D-Waveシステムに問題を投入する際に複数のアニーリングを要求する必要があります。

量子アニーリングを使用すると、大きな問題でもサンプル群が非常に高速に生成されます。

例1

頂点が5つある以下のグラフについて、最大カット(Max Cut)を求めます。

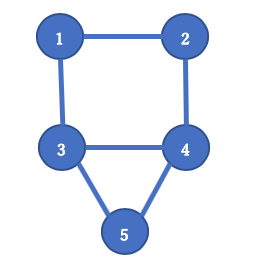
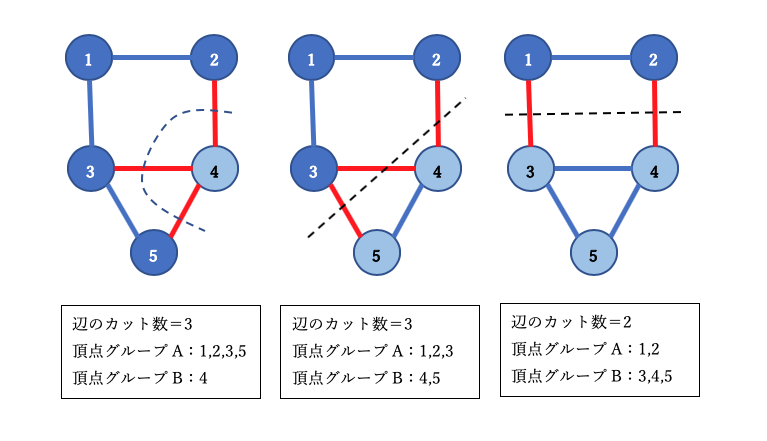
様々なカット方法がありますが、以下では、頂点のセットを2つのグループに分割する3つの異なる方法を示しています。 各グラフの赤い辺は、カットされた辺を示しており、左からカットされた辺の数は、3、3、2となります。

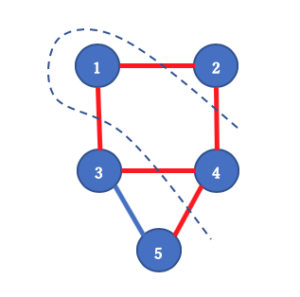
以下の頂点の組み合わせ2つのどちらも最大のカット数（5）となりそうです。（複数の最適解があります。）

• 頂点グループA： 1,4、頂点グループB： 2,3,5
• 頂点グループA： 2,3、頂点グループB： 1,4,5

それでは、実際に、D-Waveシステムでこのグラフについて最大カット(Max Cut)を求めます。
D-Waveシステムへは1回の問題投入で複数のアニーリングを要求できるため、D-Waveシステムから一度に複数の解を得ることができます。

以下のように各自のPC上にD-Wave SDKを使ってプログラムを作成し実行し、この問題を解きます。
「result=sampler.sample_qubo(Q,num_reads=1000)」の箇所でPCからD-Waveシステムへデータが転送され、量子アニーリングを設定数回分（この例では1000回）実施し、結果をPCへ戻します。

【プログラム】
# ------ Import necessary packages ----
import networkx as nx
from collections import defaultdict
from dwave.system.samplers import DWaveSampler
from dwave.system.composites import EmbeddingComposite
 
# ------- Set up our graph -------
# Create empty graph
G = nx.Graph()
 
# Add edges to the graph (also adds nodes)
G.add_edges_from([(1,2),(1,3),(2,4),(3,4),(3,5),(4,5)])　←各辺を定義してグラフ（G）生成
 
# ------- Set up our QUBO dictionary -------
# Initialize our Q matrix
Q = defaultdict(int)
 
# Update Q matrix for every edge in the graph
for u, v in G.edges:　　　　←最大カットを求めるためのQUBO（Q）をグラフ（G）から作成（※参照１）
    Q[(u,u)]+= -1          ←それぞれの頂点が持つ辺の本数のマイナス値を設定
    Q[(v,v)]+= -1          ←それぞれの頂点が持つ辺の本数のマイナス値を設定
    Q[(u,v)]+= 2           ←（※参照１）
print(Q)　 ←Qの内容をプリント
 
# ------- Run our QUBO on the QPU -------
# Set up QPU parameters
numruns = 1000　　　　　　　←アニーリング回数の設定
 
# Run the QUBO on the solver from your config file
sampler=EmbeddingComposite(DWaveSampler())　　←サンプラーを設定（D-Waveの構造にマップします）
response = sampler.sample_qubo(Q, num_reads=numruns) 　←Qをマップし、D-Waveで1000回アニーリング実施
for s,e,o,c in response.data(['sample', 'energy', 'num_occurrences', 'chain_break_fraction']):
    print(s, e, o, c)　　　←1000回のアニーリングの集計結果（頂点組み合わせと、
そのエネルギー値、出現数及びchain break fraction値（※参照2）をプリント
 
【プリント出力】配列Qの内容
defaultdict(<class 'int'>, {(1, 1): -2, (2, 2): -2, (1, 2): 2, (3, 3): -3, (1, 3): 2, (4, 4): -3, (2, 4): 2, (3, 4): 2, (5, 5): -2, (3, 5): 2, (4, 5): 2})
 
【プリント出力】頂点組み合わせパターンと、そのエネルギー値、出現数及びchain break fraction値
{1: 0, 2: 1, 3: 1, 4: 0, 5: 0} -5.0 232 0.0
    ←「1：0」＝「頂点1：選択しない」、「2：1」＝「頂点2：選択する」、「3：1」＝「頂点3：選択する」、、、
    ←頂点2,3の組み合わせのエネルギー値は「-5.0」で、1000回のうち232回出現。
    ←chain break fraction値（※参照2）は0.0。　以下同様。
{1: 1, 2: 0, 3: 0, 4: 1, 5: 0} -5.0 363 0.0
{1: 0, 2: 1, 3: 1, 4: 0, 5: 1} -5.0 203 0.0
{1: 1, 2: 0, 3: 0, 4: 1, 5: 1} -5.0 197 0.0
{1: 0, 2: 1, 3: 1, 4: 1, 5: 0} -4.0 1 0.0
{1: 1, 2: 0, 3: 0, 4: 0, 5: 1} -4.0 1 0.0
{1: 1, 2: 1, 3: 0, 4: 0, 5: 1} -4.0 2 0.0
{1: 0, 2: 0, 3: 1, 4: 1, 5: 0} -4.0 1 0.0
 
この結果から、以下の頂点の組み合わせのどれもが一番低いエネルギー値「-5.0」となりますので、「カットされる辺の本数を最大にする」2つのグループの組み合わせはこの2つのパターンとなります。

• 頂点グループA： 1,4、頂点グループB： 2,3,5
• 頂点グループA： 2,3、頂点グループB： 1,4,5

ここでは、「カットされる辺の本数を最大にする」2つのグループに属する頂点の組み合わせを求めていますので、一番低いエネルギー値「-5.0」となる解のうち、
1番目の解の{1: 0, 2: 1, 3: 1, 4: 0, 5: 0}と4番目の解の{1: 1, 2: 0, 3: 0, 4: 1, 5: 1}はどちらも、
頂点グループA： 2,3、頂点グループB： 1,4,5の組み合わせを意味しています。
2番目の解の{1: 1, 2: 0, 3: 0, 4: 1, 5: 0}と3番目の解の{1: 0, 2: 1, 3: 1, 4: 0, 5: 1}はどちらも、
頂点グループA： 1,4、頂点グループB： 2,3,5の組み合わせを意味しています。

（参照1）

この問題の目的は、辺をカットし、グラフ内の頂点を２つのグループに分割することです。したがって、各頂点にバイナリ変数を割り当てることで2つのグループに分割することができます。すなわち、バイナリ変数xiは、頂点iが一方のグループ（変数値が0）に属すかもう一方のグループ（変数値が1）に属すかを示します。

最適化しようとしている目的関数は、カットする辺の数を最大化することです。 頂点を分割（バイナリ変数の割り当て）するためにカットする辺の数をカウントするために、次の表を使って考察します。 カットされる辺の両端点はそれぞれ異なるグループに属す（片方が１なら、片方は0）ので、両端点の属すグループが異なっている辺のみをカウントします。その場合、辺(i,j)列に1を割り当て、そうでない場合は0を割り当てます。

この表から、式『x_i+x_j-2x_i x_j』によって表の辺(i,j)列を計算できることがわかります。 グラフ全体について、目的関数は次のように記述できます。ここでは、グラフ内にあるすべての辺について合計しています。

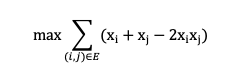
D-Waveシステムは目的関数を最小化するために使用されるため、上述の式に『-1』を乗算して、この最大化問題を最小化問題に変換する必要があります。 最終的なQUBO式は次のとおりです。

例１のグラフの場合、このQUBOは次の行列Qになります。 行列Q（Oceanを使用して辞書として実装）では、対角線に沿ってQUBOの線形項に係数を配置し、非対角線に2次項を配置します。

Q:

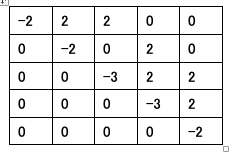
例1のPythonコードでは、ちょうど上述のQUBO式のとおりに、グラフ内のすべての辺についてループ計算し、辞書としてこの行列Qを作成しています。

（参照2）

D-WaveシステムへQUBOの埋め込みを行う際に、qubitをより多くのqubitに接続する必要がある場合、同じ値をとるようにバイアスを増やして、複数のqubitを単一のqubitとして扱います。これをチェーンと呼びます。
チェーンのバイアスが低すぎる場合、そのバイアスが原因でチェーンが破損する可能性があります（例：101111）。
チェーンを途切れないようにすることが重要です（例：111111）。チェーンを途切れないようにするために、チェーンの強度を上げることができます。
chain break fraction値がゼロではない場合、チェーンが壊れていますので、行列Qの数値を調べ、埋め込みにおいてチェーンを強制するために、チェーンの強度について、それらの数値より比較的大きな数を設定します。 この問題の場合、行列内の数値の範囲は-3〜+2であるため、チェーン破損が認められるときには、例えば、以下のように設定してアニーリングを試行します。（チェーン強度は8）
response = sampler.sample_qubo(Q, chain_strength=8, num_reads=numruns)

※例１は、https://github.com/dwavesystems/demos/tree/master/maximum-cutを参考にしています。
チェーンについては、https://docs.dwavesys.com/docs/latest/c_gs_7.htmlをご参照ください。

例2

次は、以下のグラフについて、最大カット(Max Cut)を求めます。

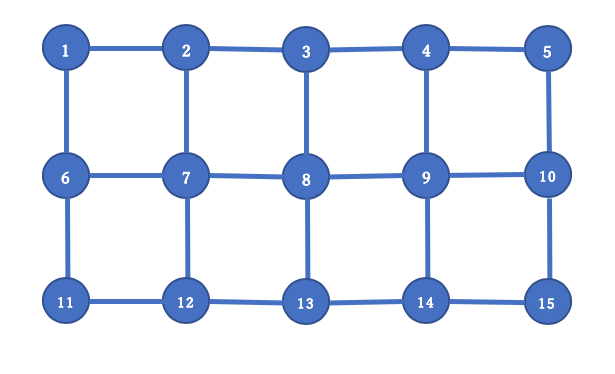
例1のプログラムの辺の定義のみを以下のように書き換えて、実行します。

G.add_edges_from([(1,2),(2,3),(3,4),(4,5),(6,7),(7,8),(8,9),(9,10),(11,12),(12,13),(13,14),(14,15),(1,6),(6,11),(2,7),(7,12),(3,8),(8,13),(4,9),(9,14),(5,10),(10,15)])

【結果】
defaultdict(<class ‘int’>, {(1, 1): -2, (2, 2): -3, (1, 2): 2, (6, 6): -3, (1, 6): 2, (3, 3): -3, (2, 3): 2, (7, 7): -4, (2, 7): 2, (4, 4): -3, (3, 4): 2, (8, 8): -4, (3, 8): 2, (5, 5): -2, (4, 5): 2, (9, 9): -4, (4, 9): 2, (10, 10): -3, (5, 10): 2, (6, 7): 2, (11, 11): -2, (6, 11): 2, (7, 8): 2, (12, 12): -3, (7, 12): 2, (8, 9): 2, (13, 13): -3, (8, 13): 2, (9, 10): 2, (14, 14): -3, (9, 14): 2, (15, 15): -2, (10, 15): 2, (11, 12): 2, (12, 13): 2, (13, 14): 2, (14, 15): 2})
{1: 1, 2: 0, 3: 1, 4: 0, 5: 1, 6: 0, 7: 1, 8: 0, 9: 1, 10: 0, 11: 1, 12: 0, 13: 1, 14: 0, 15: 1} -22.0 447 0.0
{1: 0, 2: 1, 3: 0, 4: 1, 5: 0, 6: 1, 7: 0, 8: 1, 9: 0, 10: 1, 11: 0, 12: 1, 13: 0, 14: 1, 15: 0} -22.0 549 0.0
{1: 0, 2: 1, 3: 0, 4: 1, 5: 1, 6: 1, 7: 0, 8: 1, 9: 0, 10: 1, 11: 0, 12: 1, 13: 0, 14: 1, 15: 0} -20.0 3 0.0
{1: 1, 2: 0, 3: 1, 4: 0, 5: 1, 6: 0, 7: 1, 8: 0, 9: 1, 10: 0, 11: 1, 12: 0, 13: 1, 14: 0, 15: 0} -20.0 1 0.0
 
この結果から、以下の頂点の組み合わせのどれもが一番低いエネルギー値「-22.0」となりますので、「カットされる辺の本数を最大にする」2つのグループの組み合わせはこの1つのパターンとなります。
 
頂点グループA： 1,3,5,7,9,11,13,15、頂点グループB： 2,4,6,8,10,12,14
 
ここでは、「カットされる辺の本数を最大にする」2つのグループに属する頂点の組み合わせを求めていますので、一番低いエネルギー値「-22.0」となる解のうち、
1番目の解の{1: 1, 2: 0, 3: 1, 4: 0, 5: 1, 6: 0, 7: 1, 8: 0, 9: 1, 10: 0, 11: 1, 12: 0, 13: 1, 14: 0, 15: 1}と2番目の解の{1: 0, 2: 1, 3: 0, 4: 1, 5: 0, 6: 1, 7: 0, 8: 1, 9: 0, 10: 1, 11: 0, 12: 1, 13: 0, 14: 1, 15: 0}はどちらも、
頂点グループA： 1,3,5,7,9,11,13,15、頂点グループB： 2,4,6,8,10,12,14の組み合わせを意味しています。